
在研究工程結構動力災變機理、健康監測和安全評估時,一個首先需要解決的關鍵問題就是正確地識別或監測結構的動力特性或參數,這些參數是研究結構災變機理、健康監測和安全評估的基礎和依據。參數識別屬於系統識別範疇,一般意義上講,就是在觀察到的系統輸入(激勵)和輸出(回應)資料的基礎上,對系統確定一個數學模型,要求這個模型盡可能精確地反映系統的特性,從而達到識別系統參數的目的。系統識別原本是現代控制理論研究的基本問題之一,近年以來已愈來愈在各類工程結構中顯示出潛在的應用前景,是學科滲透和結構工程專業概念拓寬的一個典型實例。
結構動力特性研究結構災變機理、健康監測和安全評估的基礎和依據
目前常用的結構參數識別方法通常可以分為兩類。一類是建立在系統輸入和輸出資料基礎上的識別方法。在工程結構振動試驗中, 這類方法需要測量結構的激勵(輸入)和動力回應(輸出),求出反應輸入-輸出關係和系統固有特性的傳遞函數,然後建立傳遞函數與系統參數之間的關係,從而識別出結構的特徵參數。另一類是僅建立在輸出資料基礎上的系統識別方法。這類方法直接利用車輛、行人、風荷載等作用於結構上的日常環境激勵作為系統的輸入,僅根據結構的回應資料完成參數的識別過程。為了便於數學處理,僅基於輸出資料的參數識別方法通常對輸入模型做了理想化假定。然而,這些理想化條件在實際工程中很難得到嚴格滿足,在陣風、車輛等環境荷載激勵下,很多時候工程結構難以避免地受到複雜激勵的作用,如有色雜訊激勵甚至是諧波激勵,實踐與理論的差異無疑會影響系統識別結果的魯棒性與準確性,甚至會導致識別出錯誤的結果。因此,有必要在系統識別階段引入新的方法來充分考慮輸入的影響,為土木工程結構動力災變和安全監測分析提供更穩健可靠的基礎和依據。
 |
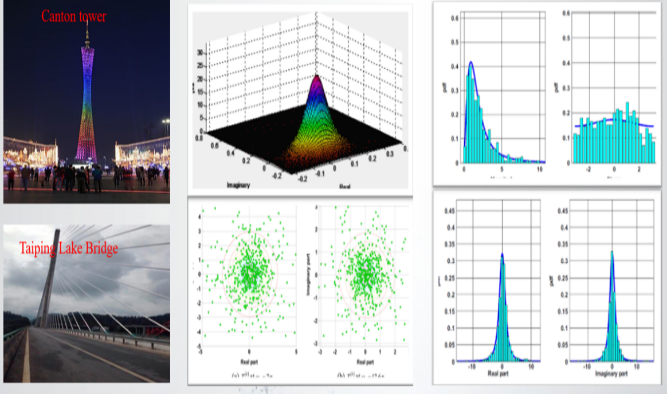 |
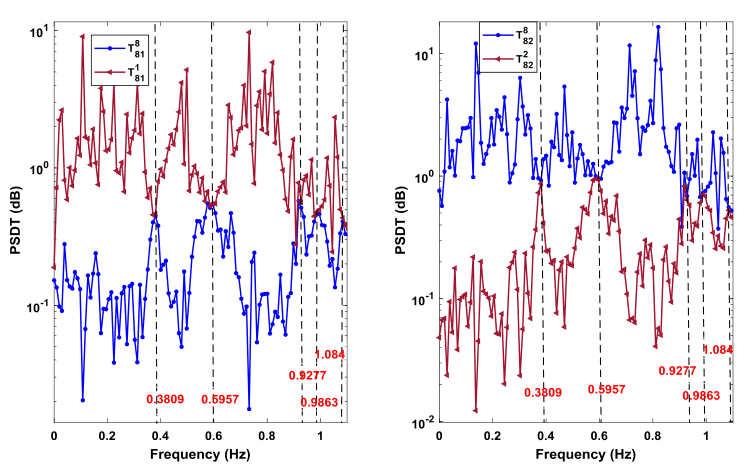
工程結構監測資料表明振動傳遞比具有獨特的物理特性和統計規律
 |
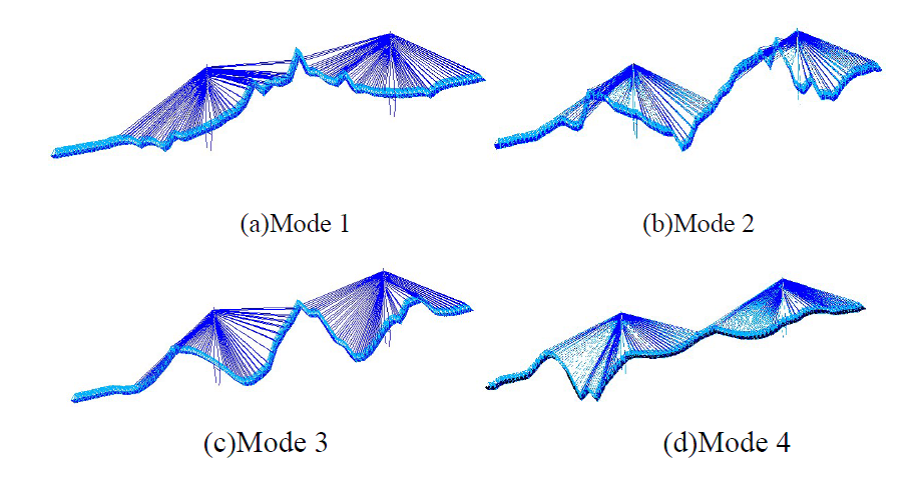 |
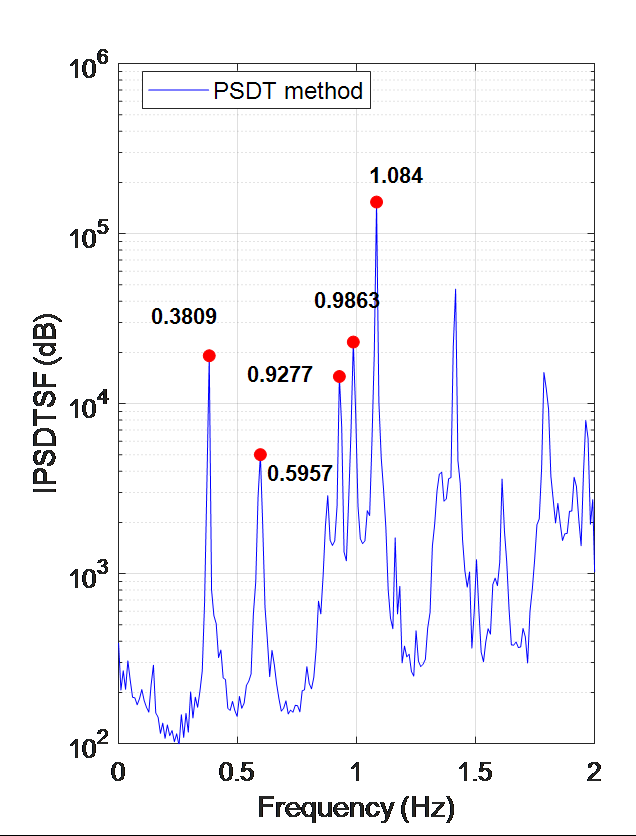
振動傳遞比之特性可以用於快速地識別複雜環境激勵下的結構動力特性
近年來,振動傳遞比函數因為其諸多優點成為了系統識別領域重要的分析手段。與頻響函數反映動力系統輸入-輸出的關係不同,振動回應傳遞比函數反映的是系統輸出-輸出之間的關係。因此,應用振動回應傳遞比函數時,系統輸入只作為動力源而不需要參與運算,因此避免了對系統荷載測量的依賴,從而有效地避免了輸入資料的測量。同時,振動回應傳遞比函數可以有效地避免對系統輸入的白色雜訊假定。通過近十餘年時間的探索,課題組在振動傳遞比的固有特性分析和參數識別方法方面取得了一系列富有創新特色的研究成果:(i)提出了功率譜傳遞比(簡稱PSDT)新概念,證明瞭複數域比例函數極限定理,揭示了PSDT在系統極點處獨立於參考輸出和激勵的位置且與兩測點的振型比值等價的物理特性;(ii)基於PSDT的物理特性,建立了PSDT驅動的結構參數識別峰值法和最小二乘複頻域方法,建立了穩定圖剔除虛假模態; (iii)證明瞭複數域比例隨機向量統計推斷定理,揭示了振動傳遞比的統計規律,建立了解析概率模型實現振動傳遞比測量不確定性表徵;(iv)基於振動傳遞比解析概率模型,提出了貝葉斯傳遞比方法實現特徵參數識別不確定性快速量化;(v)推導出了特徵參數變異係數關於不同隨機源的近似閉合解,闡明瞭不同特徵參數之間的相關程度,揭示了特徵參數不確定性的傳播機理。相關成果在國內外著名期刊發表論文12篇;曾獲省自然科學二等獎、省自然科學優秀學術論文一等獎、教育部提名國家自然科學二等獎;被澳大利亞工程院院士Hong Hao教授和上海交大國家傑青、長江彭志科教授等在內的學術同行發表的25篇論文直接跟蹤拓展,10餘篇論文在標題中直接採用了首創名詞PSDT;振動傳遞比理論在10餘座土木工程結構中得到成功應用。
REFERENCE
- Wang-Ji Yan and Wei-Xin Ren (2012): Operational modal parameter identification from power spectrum density transmissibility. Computer-Aided Civil and Infrastructure Engineering, Vol.27, No.3, pp.202-217.
- Wang-Ji Yan and Wei-Xin Ren (2013): Use of continuous wavelet transmissibility for operational modal identification. Journal of Structural Engineering, ASCE, Vol.139, No.9, pp.1444-1456.
- Wang-Ji Yan and Wei-Xin Ren (2015): An enhanced power spectral density transmissibility (EPSDT) approach for operational modal analysis: theoretical and experimental investigation. Engineering Structures, Vol. 102, pp.108-119.
- Wang-Ji Yan and Wei-Xin Ren (2016): Circularly-symmetric complex normal ratio distribution for scalar transmissibility functions. Part I: Fundamentals. Mechanical Systems and Signal Processing, Vol. 80, pp.58-77.
- Wang-Ji Yan and Wei-Xin Ren (2016): Circularly-symmetric complex normal ratio distribution for scalar transmissibility functions. Part II: Probabilistic models and validation. Mechanical Systems and Signal Processing, Vol. 80, pp.78-98.
- Wang-Ji Yan and Wei-Xin Ren (2018): Circularly-symmetric complex normal ratio distribution for scalar transmissibility functions. Part III: Application to statistical modal analysis. Mechanical Systems and Signal Processing, Vol. 98, pp. 1000-1019.
- Wang-Ji Yan, Meng-Yun Zhao, Qian Sun and Wei-Xin Ren (2019): Transmissibility-based system identification for structural health monitoring: Fundamentals, approaches and applications. Mechanical Systems and Signal Processing, Vol. 117, pp. 453-482.
- Wang-Ji Yan and Lambros Katafygiotis (2019): An analytical investigation into the propagation properties of uncertainty in a two-stage fast Bayesian spectral density approach for ambient modal analysis. Mechanical Systems and Signal Processing, Vol. 118, pp. 503-533.
